천천히 빛나는
알고리즘 : 최단 경로 알고리즘 (2) - 플로이드 워셜 알고리즘 본문
플로이드 워셜 알고리즘
모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산한다. 플로이드 워셜은 다익스트라 알고리즘과 마찬가지로 단계별로 거쳐가는 노드를 기준으로 알고리즘을 수행한다.
다익스트라 알고리즘이란?
https://shine-slowly.tistory.com/85
알고리즘 : 다익스트라(Dijkstra) 최단 경로 알고리즘 (Java로 구현)
다익스트라 최단 경로 알고리즘 최단 경로 알고리즘은 가장 짧은 경로를 찾는 알고리즘을 의미한다. 최단 경로 알고리즘 중 다익스트라 알고리즘은 다음과 같은 특징을 가지고 있다. 특정한 노
shine-slowly.tistory.com
다익스트라 알고리즘과 다른게 매 단계마다 방문하지 않은 노드 중에서 최단 거리를 갖는 노드를 찾는 과정이 필요하지 않다.
플로이드 워셜은 2차원 테이블에 최단 거리 정보를 저장한다. 플로이드 워셜 알고리즘은 다이나믹 프로그래밍 유형에 속한다.
다이나믹 프로그래밍이란?
https://shine-slowly.tistory.com/58
알고리즘 : 다이나믹 프로그래밍 (Dynamic Programming) (1)
참고 영상: https://www.youtube.com/watch?v=5Lu34WIx2Us 다이나믹 프로그래밍 (Dynamic Programming, 동적 계획법) 메모리를 적절히 사용하여 수행 시간 효율성을 향상시키는 방법 이미 계산된 결과는 별도의 메
shine-slowly.tistory.com
점화식에 맞게 삼중 반복문을 활용하여 2차원 테이블을 업데이트해주는 방식이다. 시간 복잡도가 O(n^3)이므로 노드의 개수와 간선의 개수가 많은 상황에서는 다익스트라 알고리즘을 써야하는 경우가 많다. (구현 난이도는 좀 더 낮다.)
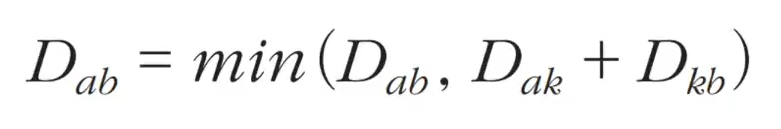
플로이드 워셜 알고리즘의 점화식이다. 각 단계마다 특정한 노드 k를 거쳐 가는 경우를 확인한다. a에서 b로 가는 최단 거리보다 a에서 k를 거쳐 b로 가는 거리가 더 짧은지 검사를 한다.
동작과정
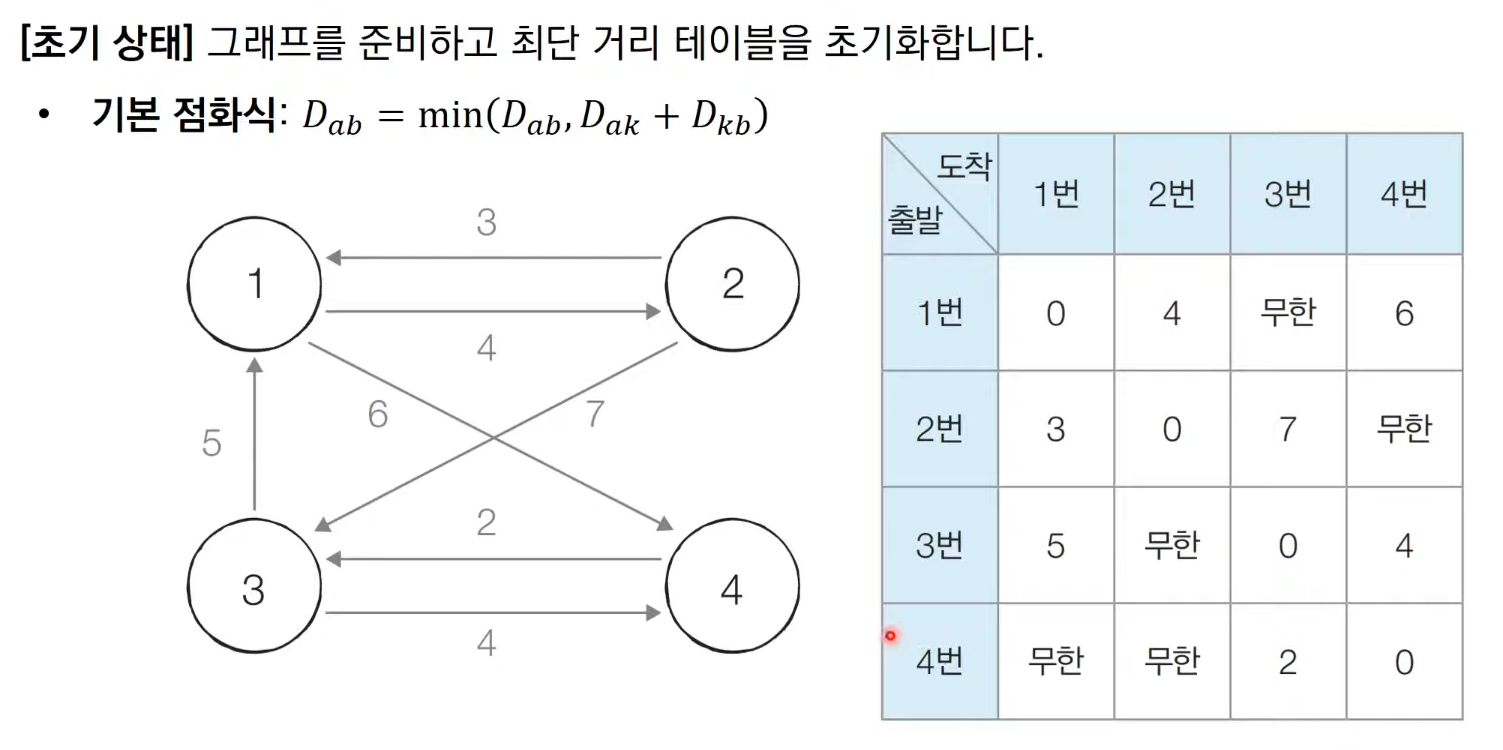
[초기 상태] 그래프를 준비하고 최단 거리 테이블을 초기화한다. 인접한 노드에 대한 정보만 담으면 된다.

[1] 1번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다. 현재 k = 1인 상황이다. a, b가 1인 상황은 제외하고 나머지 상황만 고려를 한다.

[2] 2번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다. k = 2인 상황이다. 자기 자신에서 자기 자신으로 가는 상황, a나 b가 2인 상황은 제외한다.

[3] 3번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다. 여기선 7이 갱신되었다.

[4] 모든 노드에 대해 확인하면서 해당 노드를 거쳐가는 상황을 탐색하였다.
이는 3중 반복문으로 구현할 수가 있다.
import java.util.*;
public class Main {
public static final int INF = (int) 1e9; // 무한을 의미하는 값으로 10억을 설정
// 노드의 개수(N), 간선의 개수(M)
// 노드의 개수는 최대 500개라고 가정
public static int n, m;
// 2차원 배열(그래프 표현)를 만들기
public static int[][] graph = new int[501][501];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
// 최단 거리 테이블을 모두 무한으로 초기화
for (int i = 0; i < 501; i++) {
Arrays.fill(graph[i], INF);
}
// 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
if (a == b) graph[a][b] = 0;
}
}
// 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for (int i = 0; i < m; i++) {
// A에서 B로 가는 비용은 C라고 설정
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
graph[a][b] = c;
}
// 점화식에 따라 플로이드 워셜 알고리즘을 수행
for (int k = 1; k <= n; k++) {
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
graph[a][b] = Math.min(graph[a][b], graph[a][k] + graph[k][b]);
}
}
}
// 수행된 결과를 출력
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
// 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
if (graph[a][b] == INF) {
System.out.print("INFINITY ");
}
// 도달할 수 있는 경우 거리를 출력
else {
System.out.print(graph[a][b] + " ");
}
}
System.out.println();
}
}
}중간에 삼중 포문으로 프로이드 워셜 알고리즘이 사용된 것을 알 수 있다. 플로이드 워셜은 앞서 말했듯이 노드의 개수가 500개 이상으로 주어지지 않는 경우가 많다. (1000만 되어도 10억이 넘기 때문이다)
플로이드 워셜 알고리즘의 시간복잡도는 O(n^3)이므로 최단 경로 알고리즘을 결정할 때 상황을 보고 결정해야 한다.
'STUDY > ALGORITHM' 카테고리의 다른 글
| 알고리즘 : 위상 정렬 (0) | 2024.02.23 |
|---|---|
| 알고리즘 : 최단 경로 알고리즘 (3) - 기초 문제 풀이 (미완성!!!) (0) | 2024.02.23 |
| 알고리즘 : 최단 경로 알고리즘 (1) - 다익스트라(Dijkstra) 알고리즘 (Java로 구현) (0) | 2024.02.23 |
| 알고리즘 : 다이나믹 프로그래밍 (Dynamic Programming) (2) - 기초 문제 풀이 (C++로 구현) (0) | 2023.10.20 |
| 알고리즘 : 다이나믹 프로그래밍 (Dynamic Programming) (1) (0) | 2023.10.19 |





